背包问题综合

Posted on
Words count in article: | Reading time ≈
今天学习了动态规划的背包问题，包括01背包、完全背包、多重背包、分组背包。其核心方法是构建状态表示以及状态计算，前者包括背包物品序列i，背包当前容量j，后者进行子集划分得到状态计算方程。

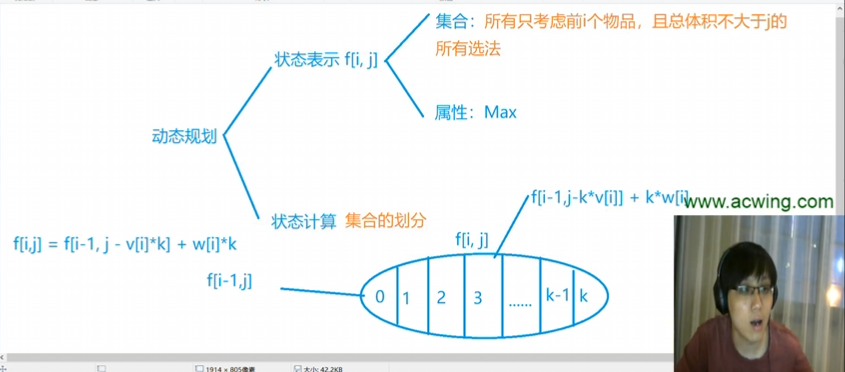
动态规划

DP：状态表示和状态计算（状态子集的划分）

状态标识：集合（只考虑前i个物品，且体积不大于j的选法）、属性

01背包问题

c++

二维
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int f[N][N];
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}
一维
1

完全背包

思路

曲线救国：1.去掉k个物品i

​ 2.求max，

将集合划分为，包含第i个，不包含第i个

前者：\(f[i][j]\)

后者：\(f[i-1][j-kv[i]]+kw[i]\)

image-20240315210232850

初步代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;
int v[N],w[N];
int dp[N][N];
int n,m;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            for(int k=0;k*v[i]<=j;k++){
                dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<(dp[n][m]);
    return 0;
}

优化

对状态计算进行优化

对于 \[ \begin{aligned} f[i][j]=max(f[i-1][j],&f[i-1][j-v]+w,f[i-1][j-2v]+2w,\ldots)\\ f[i][j-v]=max(&f[i-1][j-v],f[i-1][j-2v],\ldots) \end{aligned} \] 因此 \[ f[i][j]=max(f[i-1][j],f[i][j-v]+w) \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;
int v[N],w[N];
int dp[N][N];
int n,m;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            dp[i][j]=dp[i-1][j];
            if(j>=v[i]){
            dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);}
        }
    }
    cout<<(dp[n][m]);
    return 0;
}

完全背包和01背包比较

image-20240315212746459

多重背包

加入 k<=s[i]的额外条件即可，其他与多重背包完全一致

初步代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i]>>s[i];
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            for(int k=0;k*v[i]<=j&&k<=s[i];k++){
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<(f[n][m]);
}

优化

二进制离散优化

将每个具有 \(s\) 个的物品，分解成 \(\log_2 s\) 堆物品，例如1 ,2,4等等，这些必然可以组合0到s的任意数，因此这样的分解是和原问题等效的。

将 \(n\) 种物品全都分解

最后再使用01背包问题解法即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<iostream>
#include<algorithm>
using namespace std;
const int N=25000,M=2010;
int n,m;
int v[N],w[N];
int f[N];
int cnt;
int main(){
    cin>>n>>m;
    for (int i=1;i<=n;i++){
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;
        while(k<=s){
            cnt++;
            v[cnt]=a*k;
            w[cnt]=b*k;
            s-=k;
            k*=2;
        }
        if(s>0){
        cnt++;
        v[cnt]+=a*s;
        w[cnt]+=b*s;
    }
    }
    
    n=cnt;
    for(int i=1;i<=n;i++){
        for(int j=m;j>=v[i];j--){
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m]<<endl;
    
}

组合背包

思路： 考虑多重背包的思想，仅仅将每个物品选几个替换成——选当前组的哪一个物品

初始代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int v[N][N],w[N][N];
int f[N][N];
int index[N];
int n,m;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>index[i];
        for(int j=0;j<=index[i]-1;j++){
            cin>>v[i][j]>>w[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j];//注意注释
            for(int k=0;k<=index[i]-1;k++){
                if(v[i][k]<=j){
                f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
                }
            }
        }
    }
    cout<<f[n][m]<<endl;
}

在更新状态时，需要考虑每个组内选择每个物品的情况，且在同一个背包容量下，应该是在上一个状态的基础上考虑新增物品的价值，而不是直接使用f[i][j] = f[i-1][j]来更新。这一行在循环开始前只需设置一次，而不是在每次考虑新物品时都重置。

优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int v[N][N], w[N][N];
int f[N]; // 使用一维数组进行优化
int index[N];
int n, m;

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i++) {
        cin >> index[i];
        for(int j = 0; j < index[i]; j++) {
            cin >> v[i][j] >> w[i][j];
        }
    }

    // 遍历所有组
    for(int i = 1; i <= n; i++) {
        // 从大到小遍历所有背包容量
        for(int j = m; j >= 0; j--) {
            // 遍历当前组内所有物品
            for(int k = 0; k < index[i]; k++) {
                if(v[i][k] <= j) {
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
                }
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}