2 基于关键故障特征筛选的朴素贝叶斯故障诊断算法

2.1 引言

2.2 传统贝朴素贝叶斯分类器

不足：

没有对系统变量进行选择，有利于分类的、显著的故障信息容易在多个条件概率乘积中被掩盖不利于分类性能的提高
独立性假设在实际问题可能并不成立

2.3 变量选择与特征提取

定义：

2.3.1 基于互信息的变量选择方法

变量选择的评价标准，对所选变量或变量组合优劣程度做评价的指标

距离度量
一致性度量
依赖性度量
互信息度量

互信息度量：即可对线性也可非线性度量，无需知道样本数据的先验分布知识，不依赖数据分布情况

Shannon的信息理论，通过概率同济方法计算信息熵和互信息: \[ H(V)=-\int_vp(v)\log p(v)dv \] 给定两个随机变量 \(V_1\) 和 \(V_2\) ，其联合信息熵 \(H(V_1,V_2)\) 可由联合概率分布 \(p(v_1,v_2)\) 进行描述 \[ H(V_1,V_2)=-\iint_{v_1,v_2}p(v_1,v_2)\log p(v_1,v_2)dv_1dv_2 \] 互信息定义:两个随机变量共同包含的信息量 \[ \begin{align} I(V_1,V_2)&=H(V_1)-H(V_1|V_2)=H(V_2)-H(V_2)-H(V_2|V_1)\\ &=\iint_{v_2,v_1}p(v_1,v_2)\log {\frac{p(v_1,v_2)}{p(v_1)p(v_2)}}dv_1dv_2 \end{align} \]

2.4 过程

计算单变量互信息，选取最大的，加入到\(V_D\)
选取剩余的 \(J-i\) 个，分别计算多变量与故障类别的互信息，选取最大的，加入到 \(V_D\)
直到 \(i==J\)
按照 \(V_D\) 的顺序，每次增加一个变量放入变量矩阵中，通过ICA独立化，特征离散化，得到 \(k\) 个离散区间，计算训练数据在每个类别的概率，得到概率表，验证模型分类性能
重复4，直到所有变量都完成建模，得到分别有 \(1,2,\ldots,n\) 个变量的模型，进行排序，选择最好的模型

3 基于动静态信息协同分析的分布式贝叶斯网站在线故障诊断

3.1 引言

混合的故障特性使得单一静态故障信息对故障难以全面描述

3.2 慢特征分析

慢特征分析 (Slow Feature analysis,SFA) 是一种有效提取动态信息的方法，从时间序列中提取出随时间变化尽可能慢的波动特征

SFA算法如下

设第 \(j\) 个时间序列 \(x_j(t)\) 经过投影后输出为 \(y_j(t)\) ，则 \(y_j(t)\) 表示： \[ y_j(t)=g_j(x(t)) \] 其中 \(g_j(\cdot)\) 是变化方程

SFA是为了找到变化尽可能缓慢的特征，其目标函数为 \[ min\quad \Delta(y_i)=\langle \dot y_i^2\rangle_t \] 约束条件 \[ \langle y_j\rangle_t=0\\ \langle y_j^2\rangle_t=1\\ \forall i<j,\langle y_iy_j\rangle_t=0 \] 表面将常量作为输出结果以及保持变量不存在相关关系，即所得到的慢特征之间不存在冗余信息

因此输出的特征按照等级排序，第一个特征是最慢的特征

3.3 基于动静态协同的分布式贝叶斯网络的在线故障诊断方法

首先提取关键静态故障信息，对所有故障类型进行初步诊断
利用SFA提取多个故障的动态信息，并与关键静态信息相结合
协同分析提取丰富的故障特性，基于不同故障特性进行分布式建模，建立诊断子网

3.3.1 分布式贝叶斯网络离线建模

3.3.3.1 基于SFA的离线划分准则（SFA-PC）

SFA-PC的设计思路是将各个故障类型根据动态故障信息的快慢进行分子组，将混杂的信息进行有效解耦，后续对每个子组建立诊断子网

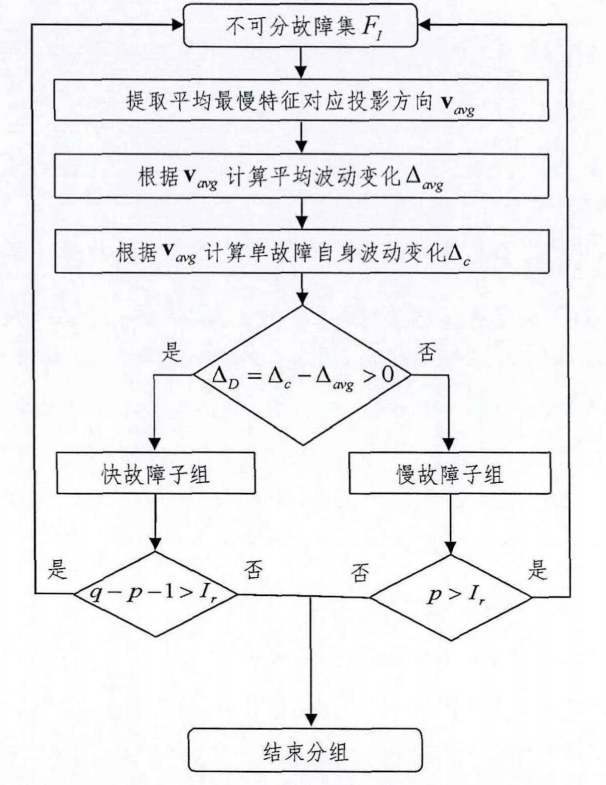
构建全局话故障诊断网络模型（GBN）
将不可分故障集进行子组划分
建立精细化的局部故障诊断子网模型（PBN）

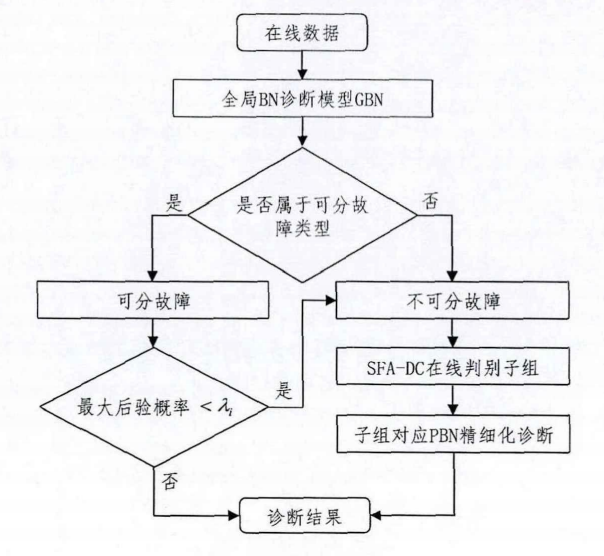
3.3.2 分布式贝叶斯网络在线故障诊断

将 \(x_t\) 输入全局诊断网络，如果是可分的，则计算最大后验概率（正确概率）是否小于阈值，如果小于阈值，则划分为不可分故障。如果大于，则得到诊断结果
如果是不可分的，通过SFA-DC在线判别子组，根据子组对应的PBN进行诊断

4 基于因果分析的多层次贝叶斯网络根源故障诊断方法研究

4.1 引言

非平稳因素：方差和均值随着时间变化的变量成为非平稳变量，过程称为非平稳过程

非平稳因素对追溯故障根源有不利影响

用差分消除非平稳特性的影响，但会损失有效的过程信息

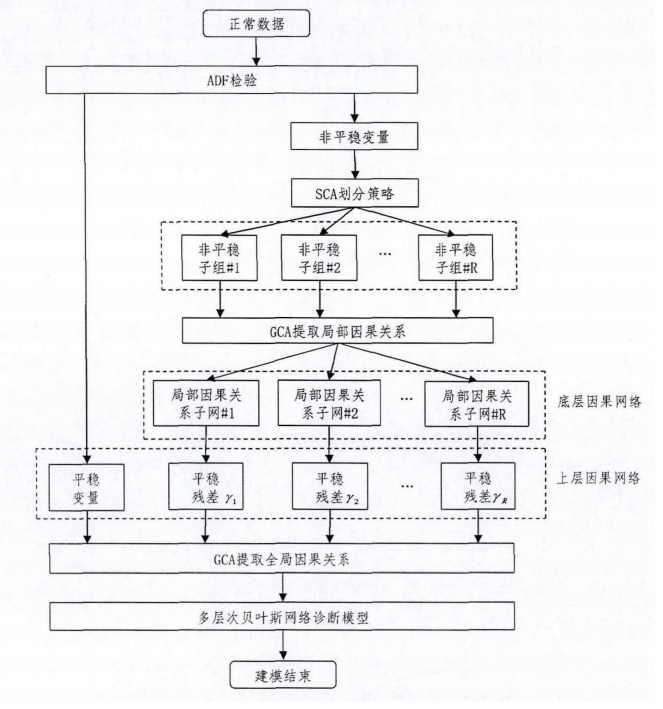
提出一种基于精细化因果分析的多层次贝叶斯网络模型，用于根源故障变量的追溯和故障传播路径的识别

首先将非平稳变量和平稳变量分离，构建两层因果诊断网络
底层由诊断子网组成，对非平稳变量进行分组，提取局部潜在因果关系，对故障信息的传递进行精细化描述，避免非平稳性带来的伪回归
上层网络用于描述全局因果关系，通过集成诊断子网的因果关系，挖掘完善的整体因果关系结构

4.2 格兰杰因果分析

格兰杰因果分析简述：

构建模型，为变量 \(X\) 和 \(Y\) 建立时间序列模型
增加滞后项，在预测变量 \(Y\) 的模型中包含变量 \(X\) 的滞后项
统计检验，进行 \(F\) 检验来评估加入 \(X\) 的滞后项是否显著提高了对 \(Y\) 的预测能力
因果关系判断

假设 \(x_1(t)\) 和 \(x_2(t)\) 是两个变量序列，那么利用不同历史数据对变量 \(x_1(t)\) 预测可表示为： \[ \begin{align} x_1(t)&=\sum_{i=1}^q\alpha _{1,i}x_1(t-i)+\sum_{j=1}^q\sigma_{1,j}x_2(t-j)+\eta_1\\ x_1(t)&=\sum_{i=1}^q\alpha _{2,i}x_1(t-i)+\eta _2 \end{align} \] 前者表示的是用 \(x_1(t)\) 和 \(x_2(t)\) 的历史数据共同表示预测 \(x_1(t)\) 的全模型，后者表示仅用 \(x_1(t)\) 进行预测

\(\alpha\ \delta\) 是模型参数，\(\eta\) 是对应模型的残差， \(q\) 表示时延长度，通过比较两者残差可以得到因果关系的判别依据 \[ FG=\frac{(\eta_2-\eta_1)/q}{\eta_1/(n-2q-1)} \] 当 \(FG\) 小于0.05时， \(x_2(t)\) 是 \(x_1(t)\) 的格兰杰原因

4.3 稀疏协整分析

协整分析(Cointegration analysis)简述：

如果两个或多个时间序列虽然自身是平稳的，但是他们的线性组合可以是平稳的，那么这些序列是协整的

传统CA中所求协整向量与所有非平稳项链有关，导致描述局部依赖关系的协整信息被掩盖

无法准确地捕捉到仅在变量的子集之间存在的细微但重要的依赖关系

稀疏协整算法（Sparse cointegration analysis）简介：

加入了惩罚函数，获得稀疏的协整向量

更能挖掘局部的协整关系信息，因此其得到的因果关系更具有解释性

4.4 面向非平稳过程的非精细化因果分析建模

4.4.1 底层因果关系网络构建

对于正常数据进行ADF检验（Augmented Dickey-Fuller）得到两个数据集，非平稳和平稳
将非平稳变量根据协整关系的强度进行分组
- 利用SCA计算稀疏协整矩阵
- 计算每个稀疏协整向量对应的平稳残差序列
- 利用ADF检验评估每个平稳残差序列的稳定性，越小越稳定
- 根据通统计量 \(T_l\) 进行变量分组，将 \(T_l\) 降序排列，保留最小的统计量对应的稀疏协整向量，该向量中非零稀疏对应的非平稳变量被划分为一组，加入 \(G\) 中
- 更新代分组的变量集 \(X_w\) ，迭代，指导 \(X_w\) 中的变量数目为0
利用GCA对每个变量子组分别求变量的因果关系，构建局部的因果关系子网

4.4.2 上层因果关系的构建

计算每个子组的平稳残差序列 \(\gamma_i\) ，\(i\) 表示第 \(i\) 个子组
利用GCA提取集合中所有平稳变量和平稳残差序列间的因果关系

《基于关键故障特征筛选的朴素贝叶斯故障诊断算法》的论文总结