贝叶斯分类器

基础知识

先验概率 \[ P(y=y_i)\\ \sum_{i=1}^c P(y_i)=1 \]

后验概率

给定观测向量 \(x\) ，某个特定类别的概率 \(P(y|x)\)

贝叶斯定理 \[ \begin{align} P(y|x)&=P(x|y)P(y)\\ &=\frac{P(x|y)P(y)}{P(x)}\\ &=\frac{p(x|y)P(y)}{\sum_ip(x|y_i)p(y_i)} \end{align} \] 最大后验概率\(MAP\) 的类别作为预测结果 \[ y^*=arg\ maxP(y_i|x)\\ \begin{cases} y_1&if\quad P(y_1|x)>P(y_2|x)\\ y_2&if\quad P(y_2|x)>P(y_1|x) \end{cases} \]

朴素贝叶斯

基本方法

条件独立性假设

假设 \(x\) 之间相互独立，则 \[ \begin{align} P(X=x|Y=c_k)&=P(X^{(1)}=x^{(1)},\ldots ,X^{(n)}=x^{n}|Y=c_k)\\ &=\prod_{i=1}^nP(X^{(j)}=x^{(j)}|Y=c_k) \end{align} \] 将上式子代入贝叶斯定理 \[ P(Y=c_k|X=x)=\frac{P(Y=c_k)\prod _jP(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_kP(Y=c_k)\prod_jP(X^{(j)}=x^{j}|Y=c_k)} \] 考虑到对于所有的 \(c_k\) 分母都相同

因此贝叶斯分类器目标函数是 \[ y=arg\ \underset{c_k}{max}P(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}|Y=c_k) \] 应用极大似然估计法求相应的概率：

先验概率 \(P(Y=c_k)\) 的极大似然估计是： \[ P(Y=c_k)=\frac{\sum_{i=1}^NI(y_i=c_k)}{N},k=1,2,\ldots,K \] 条件概率的极大似然估计： \[ P(Y=c_k)=\frac{\sum_{i=1}^NI(y_i=c_k)}{N},k=1,2,3,\ldots,K\\ P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^NI(x_i^{(j)},y_i=c_k)}{\sum_{i=1}^NI(y_i=c_k)}\\ j=1,2,\ldots,n;l=1,2,\ldots,S_j;k=1,2,\ldots,K \]

说明

\(N\) 是样本的总数
\(I\) 是指示函数，当条件为真则取值为 \(1\) ，否则为 \(0\)
\(n\) 表示样本的数量
\(S_j\) 表示第 \(j\) 个特征可能取值的数量
\(K\) 表示类别的总数
\(x_i^{j}\) 表示第 \(i\) 个样本的第 \(j\) 个特征的值
\(y_i\) 表示第 \(i\) 个样本的类别标签

朴素贝叶斯法的参数估计

输入：

训练数据集

\[ T={(x_1,y_1),(x_2,y_2),\ldots,(x_N,y_N)} \]

\(x_i^{(j)}\) 第 \(i\) 个样本的第 \(j\) 个特征 \[ x_i=(x_i^{(1)},x_i^{(2)},\ldots,x_i^{(n)}) \] \(a_{jl}\) 第 \(j\) 个特征可能取的第 \(l\) 个值 \[ x_i^{(j)}\in {a_{j1},a_{j2},\ldots,a_{(jS_i)}} \]

输出

\(x\) 的分类

\(y_i\in {c_1,c_2,\ldots,c_K}\)

步骤

计算先验概率和条件概率

\[ P(y=c_k)=\frac{\sum_{i=1}^NI(y_i=c_k)}{N},k=1,2,\ldots,K\\ P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^NI(x_i^{(j)}=a_{jl},y_i=c_k)}{\sum_{i=1}^NI(y_i=c_k)}\\ j=1,2,\ldots,n;l=1,2,\ldots,S_j;k=1,2,\ldots,K \]

对于示例计算

对于给定的示例 \(x=\left(x_i^{(1)},x_i^{(2)},\ldots,x_i^{(n)}\right)^T\)

计算 \[ P(Y=c_k)\prod_{j=1}^nP(X^{(j)}|Y=c_k),k=1,2,\ldots,K \]

确定 \(x\) 的类别

\[ y=arg\ \underset {c_k}{max}P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k) \]

应用示例

在下面这张表格中，在某些情况下我们是否应该打网球。

给定在某特定天气参数情况下，判断我们是否应该打网球

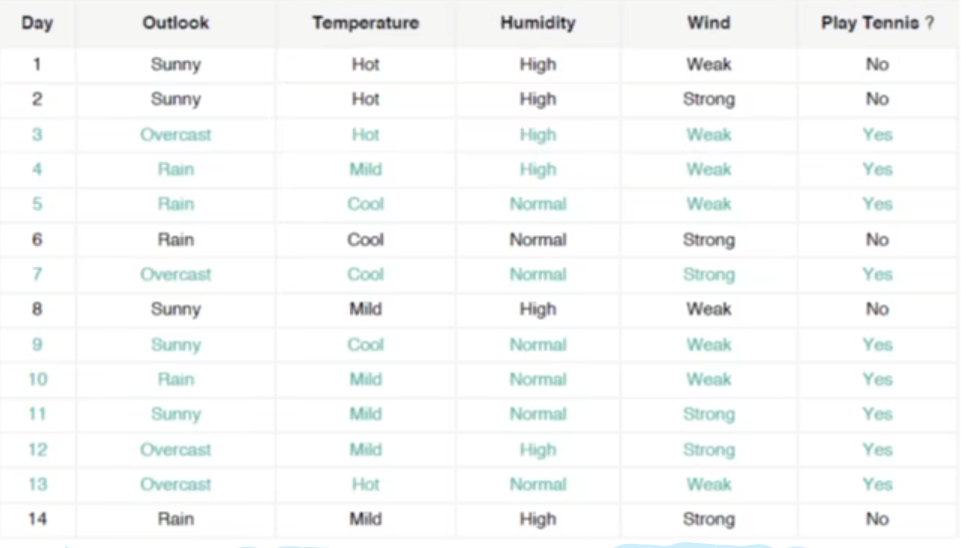
求不同特征维度下的条件概率

例如在outlook维度下， \[ P(X_{sun}^{out}|Y=yes)=\frac 29\\ P(X_{over}^{out}|Y=yes)=\frac 49\\ \ldots\ldots\\ P(X_{sun}^{out}|Y=no)=\frac 35\\ \ldots\ldots \]

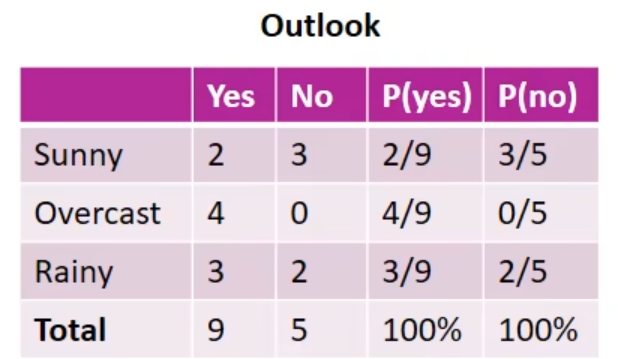
对于 \(x=(sunny,how,normal,weak)\) ， \[ y^*=arg \underset{y\in {yes,no}}{max}P(y)P(sunny|y)P(hot|y)P(normal|y)P(weak|y) \] 当 \(y=no\) 时，代入进行计算得到 \(0.0141\)

当 \(y=yes\) 时，带入进行计算得到 \(0.0069\) ，因此选择 \(no\)

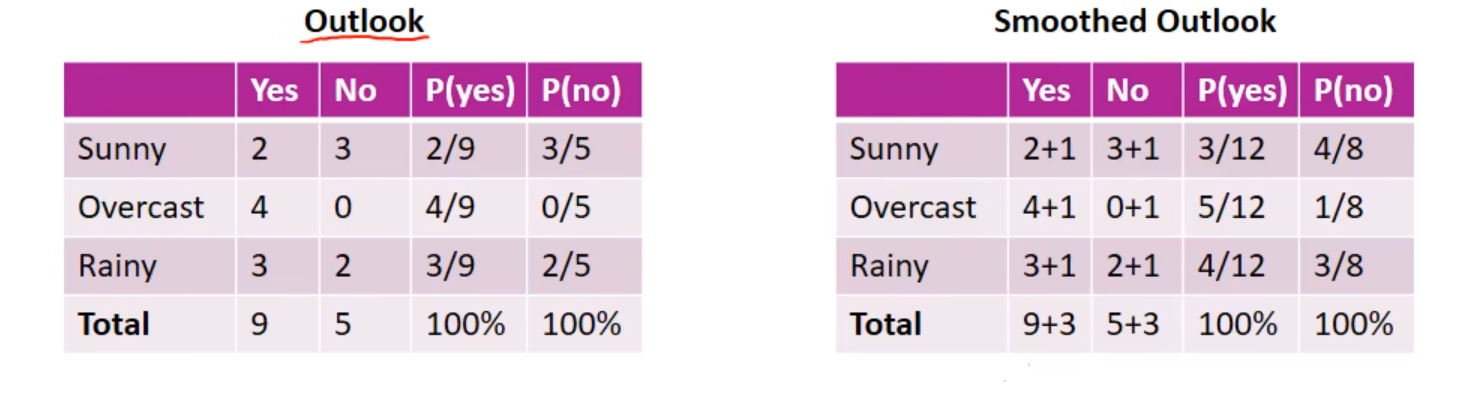
平滑处理

考虑到极大似然估计可能会出现所要估计的概率值为0的情况，这时为影响到后续概率的计算结果，使分类产生偏差

解决：采用拉普拉斯平滑 \[ \hat P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^NI(x_i^{(j)},y_i=c_k)+1}{\sum_{i=1}^NI(y_i=c_k)+{S_j}}\\ \hat P(Y=c_k)=\frac{\sum_{i=1}^NI(y_i=c_k)+{1}}{N+{K}} \]

连续特征处理

假定数据在给定类别下遵循一定的分布，例如假设数据遵循高斯分布，称为高斯朴素贝叶斯分类器

通过这种假设，根据连续特征的实际观测计算出给定类别下该值的概率密度，进而用于计算后验概率，做出分类决策