初始化博客

在cmd中输入

1	hexo init blog_test

此时便创建了一个blog_test文件夹

输入

1	cd blog_test

部署主题

此时进入该博客文件夹

输入以下，部署主题，我采用的是next主题，当然这里也可以替换别的主题

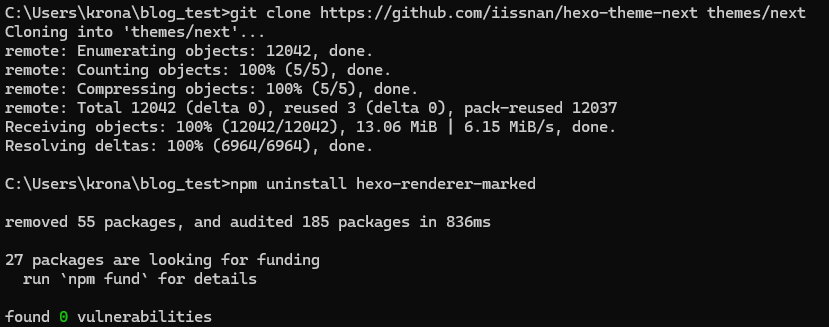
1	git clone https://github.com/iissnan/hexo-theme-next themes/next

在当前目录下找到_config.yml文件，此文件为hexo配置文件，搜索theme

改为

1	theme: next

此时主题配置完毕

公式配置

使用 \(MathJax\) 进行数学公式渲染，需要使用你需要使用 hexo-renderer-pandoc 或者 hexo-renderer-kramed （不推荐）作为 Hexo 的 Markdown 渲染器。

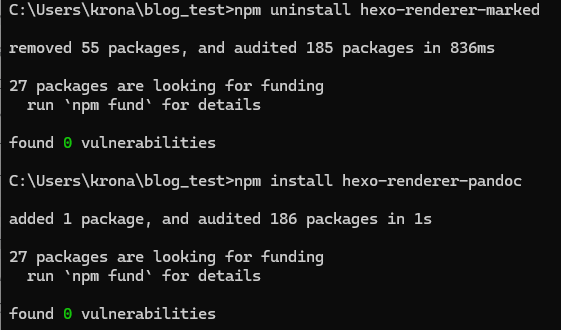
首先，卸载原有的渲染器hexo-renderer-marked，并安装上述渲染器其中一个，我这里推荐前者，因为后者还要对行内公式配置文件进行修改。

1 2	npm uninstall hexo-renderer-marked npm install hexo-renderer-pandoc

然后在 next/_config.yml 中将 mathjax 的 enable 打开

enable均改为true，per_page均改为false（这样就不用在每篇文章开头加mathjax: true），并且将cdn替换，这里的cdn非常重要，为一种分布式网络，旨在通过在多个地理位置分布的服务器上缓存网站的静态资源（如HTML页面、图片、视频、样式表和JavaScript文件），从而加快内容向用户的传输速度。当用户访问一个使用CDN服务的网站时，他们会从距离最近的服务器接收内容，这样可以显著减少公式加载时间

在大部分的博客公式配置中，都没有强调，复制粘贴时要保留这个cdn，否则公式将以latex源码的形式呈现，而不会显示公式。

这里切换cnd的目的是，切换的cdn有更好的公式渲染效果

譬如对于处于底部的大括号的显示，官方cdn将会无法显示

1	cdn: //cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.4/MathJax.js?config=TeX-MML-AM_CHTML #best one

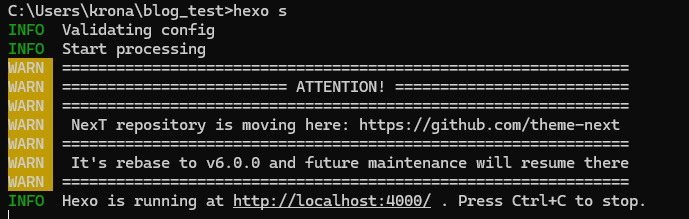
此时输入进行测试

hexo s

那么你会得到乱码的网页

1
2
3

{% extends '_layout.swig' %} {% import '_macro/post.swig' as post_template %} {% import '_macro/sidebar.swig' as sidebar_template %} {% block title %}{{ config.title }}{% if theme.index_with_subtitle and config.subtitle %} - {{config.subtitle }}{% endif %}{% endblock %} {% block page_class %} {% if is_home() %}page-home{% endif -%} {% endblock %} {% block content %}
{% for post in page.posts %} {{ post_template.render(post, true) }} {% endfor %}
{% include '_partials/pagination.swig' %} {% endblock %} {% block sidebar %} {{ sidebar_template.render(false) }} {% endblock %}

这是因为7.0版本的hexo没有安装swig，需要输入

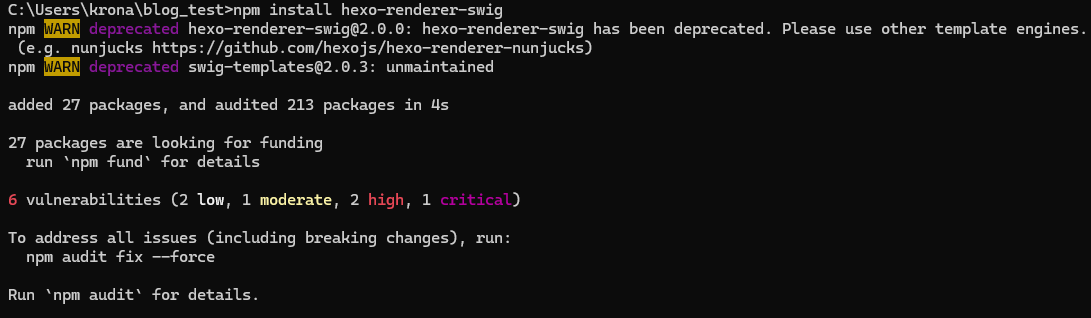
1	npm install hexo-renderer-swig

此时会有安全警告，可以无视

将带有公式的.md文件放在blog_test/resource/_posts中，然后输入以下，进行博客的公式显示测试

hexo s

此时进入

如果你能看到这样简洁优美的公式，那么恭喜，you are done!!!!

格林定理\((Green's\ Theorem)\): \[ \oint_C(L\ dx+M\ dy=\iint_D \left(\frac{\partial M}{\partial x}-\frac{\partial L}{\partial y}\right)dA \]

\[ \oint_C (L dx + M dy) = \iint_D \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right) dA \]

\[ \oint_C(Ldx+Mdy)=\iint_D\left( \frac{\partial M}{\partial x}-\frac{\partial L}{\partial y} \right)dA \]

\[ J_n(x)=\frac{1}{\pi}\int_{0}^{\pi}cos(n\tau-xsinx)d\tau \]

\[ G(s)=\left(\begin{matrix}\frac{1}{s}&0\\\frac{1}{s^2+3s-4}&\frac{1}{s+4}\end{matrix}\right) \]

\[ \underline{F(s)}\\ \overline{F(s)}\\ \bar{F(s)}\\ \hat{F(s)}\\ \tilde{F(s)}\\ \vec{F(s)} \]

\[ \begin{align*}\underline{Y(s)}&=\underline{F_0}(s)(\underline{W}(s)-\underline{Y}(s))\\ (\underline{I}+\underline{F_0}(s))Y(s)&=\underline{F_0}(s)\underline{W}(s)\\ &\Downarrow 假设可逆\\ \underline {Y}(s)&=\underbrace{(I+\underline{F_0}(s))^{-1}\cdot \underline{F_0}(s)}\cdot \underline{W}(S) \end{align*} \]

参考